论文阅读

A Low Complexity Algorithm with O($\sqrt{T}$) Regret and O(1) Constraint Violations for Online Convex Optimization with Long Term Constraints（未完待续）

题目：A Low Complexity Algorithm with O($\sqrt{T}$) Regret and O(1) Constraint Violations for Online Convex Optimization with Long Term Constraints

出处：JMLR

时间：2020

作者：Hao Yu eeyuhao@gmail.com
Department of Electrical Engineering
University of Southern California
Los Angeles, CA, 90089-2565, USA

Michael J. Neely mjneely@usc.edu
Department of Electrical Engineering
University of Southern California
Los Angeles, CA, 90089-2565, USA

摘要：

本文研究了复杂约束集上的在线凸优化问题，该问题通常由多个功能约束和一个集合约束组成。传统的在线投影算法（Zinkevich, 2003）由于投影操作潜在的高计算复杂度而难以实现。在本文中，我们放宽了功能约束，允许它们在每一轮被违反，但仍然要求它们在长期内得到满足。Mahdavi等人（2012）首先考虑了这种类型的宽松在线凸优化（具有长期约束）。先前的工作提出了一种算法，对一般问题实现O($\sqrt{T}$)遗憾和O($T^{3/4}$)约束违反，以及另一种算法，当约束集可以由有限个线性约束描述时，实现遗憾和约束违反的O($T^{2/3}$)界。Jenatton等人（2016）最近的扩展可以实现O($T^{max\{\theta,1-\theta\}}$)遗憾和O($T^{1-\theta/2}$)约束违反，其中θ 属于(0，1).本文提出了一种新的简单算法，与先前的工作相比，该算法的性能有所提高。新算法实现了一个O($\sqrt{T}$)的后悔界，违反了O(1)个约束。

关键词：在线凸优化，长期约束，遗憾边界，约束违反边界，低复杂度

结论：

与摘要基本一致。

研究背景

  • 在线凸优化问题：在线优化和学习是在不确定情况下进行决策的多轮过程。在线凸优化中，决策是从已知凸集选择，每轮会揭示凸损失函数。目标是选择一个决策序列，使累积损失与任何固定决策的损失相比具有竞争力，常用 T 轮后悔（Regret）来衡量算法性能。
  • 投影复杂性问题：对于复杂约束集的在线凸优化，传统的在线投影算法因投影操作计算复杂而难以实施。例如当约束集通过多个函数约束描述时，每轮投影操作可能需要求解复杂的凸规划，导致计算和存储负担重。
  • 长期约束的引入：为了完全规避投影算子中约束带来的计算挑战，一种称为具有长期约束的在线凸优化被考虑。在这种变体中，复杂的函数约束被放松为软长期约束，即不要求每轮都满足约束，只要求约束违反量（即约束函数值的总和）增长是次线性的。

研究目的

设计一种新的算法，用于具有长期约束的在线凸优化问题，该算法要在降低计算复杂度的同时，实现比现有算法更好的后悔界（Regret bound）和约束违反界（Constraint violation bound）。

论文贡献

  • 新的算法：提出一种新算法，在满足一定假设条件下，对于具有长期约束的在线凸优化问题，能够实现$O(\sqrt{T})$的后悔界和$O(1)$的约束违反界（不随T增长），相比之前的工作（Mahdavi等人，2012；Jenatton等人，2016）性能有所提高。
  • 解决开放问题：该算法是第一个在保持$O(\sqrt{T})$后悔界的同时，减少与多个约束相关的复杂性，并实现严格优于$O(T^{3 / 4})$的约束违反界的算法，对Mahdavi等人（2012）提出的开放问题给出了肯定答案。 -
  • 算法适应性强：算法与确定性凸规划和动态队列网络中的随机优化技术相关。并且在放松某些假设条件下，算法仍然能够取得较好性能，具有很强的适应性。

相关工作

如摘要所示，本文算法优于该方面的其他算法。

论文方法

方法一

方法二

方法三

实验与结果

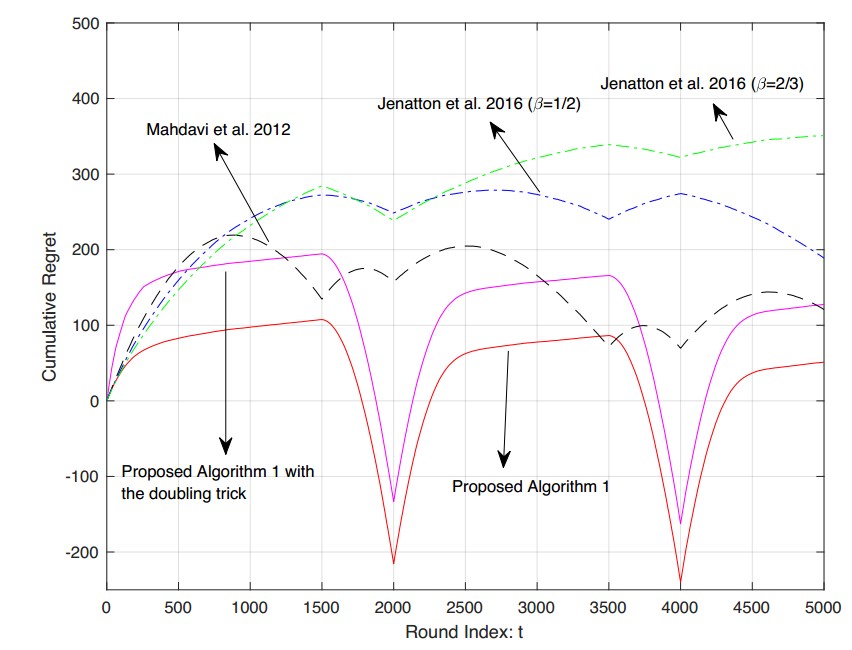
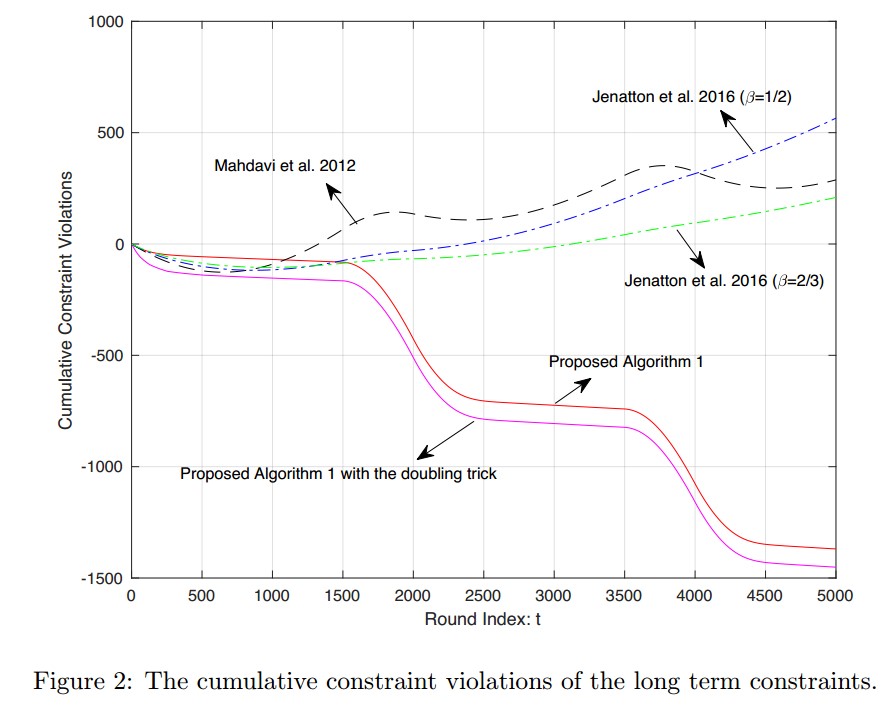
本论文通过数值实验来验证我们的算法的性能。

论文的结果如下：

个人想法

引用内容（自用）：